关于这几个函数的文章比比皆是,这是OpenGL的入门函数,但我想我讲的将不同于目前网上的文章。
OpenGL中的坐标用齐次坐标表示,即(x,y,z)表示成(x',y',z',h),其中x=x'/h; y=y'/h; z=z'/h. 通常h取1. 比如空间中的点(2,3,4),在OpenGL中将表示成(2,3,4,1). 齐次坐标表示方式适合于矩阵运算,也很方便地表示了无穷远的点,比如(1,0,0,0)就表示x轴上无穷远的点,因为1/0是无穷大,这里约定0/0=0.
接着要说点矩阵(线性代数)的知识。OpenGL里面的平移、旋转、缩放等变换均是线性变换,用矩阵相乘来表示。以平移变换为例,请见官方对glTranslatef函数的说明。假设有点(3,3,3),如果把该点沿x轴移动2单位,沿y轴移动3单位,沿z轴移动4单位,那么该点会是(3+2, 3+3, 4+4) = (5,6,7). 用矩阵表示是:
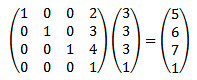
左边的矩阵称为平移变换矩阵,若把2、3、4换成x、y、z,则用它乘以一个齐次坐标表示的向量,就可以将该向量平移(x,y,z). 旋转变换和缩放变换都像平移变换一样可用一个矩阵来表示。这里可以不用理会这些矩阵长什么样,只需清楚它们乘以一个齐次坐标表示的向量,就可以使该向量发生需要的变换。
把平移变换矩阵记为T(x,y,z),旋转变换矩阵记为R(x,y,z,s),表示绕向量(x,y,z)旋转s角度;把向量记为X。这里只需要知道它们是矩阵就行了,现在要把一个点X,如(3,3,3,0),移动(2,2,2)单位,再绕y轴旋转30度角,用矩阵表示即R(0,1,0,30)*T(2,2,2)*X,可以理解为离X最近的矩阵最先作用。理解这个顺序很重要,这样,所有变换都可以用一串矩阵的相乘来表示,计算机里面也确实是这么做的。
介绍完基本的数学知识,下面说OpenGL的作用机制。OpenGL有个变换矩阵堆栈,堆栈就像子弹夹一样,先进的后出。OpenGL中的每个向量,在被定义之后进入到OpenGL世界中,都必须先乘以这个变换矩阵堆栈的栈顶变换矩阵。如下图所示:
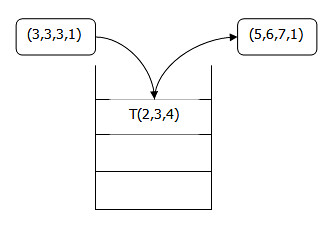
理解完上面的知识,再来理解glLoadIdentity、glTranslatef、glRotatef这些函数干了什么就容易多了。这些函数就是对这个堆栈的操作:
-
glTranslatef:将T(x,y,z)右乘与堆栈的栈顶变换矩阵。右乘的解释,假设目前栈顶变换矩阵为M,那么就相当于把M修改为M*T.
-
glRotatef :将R(x,y,z,s)右乘与堆栈的栈顶变换矩阵。
-
glLoadIdentity:将堆栈的栈顶变换矩阵设置成单位矩阵。
-
glPushMatrix:将堆栈的栈顶变换矩阵复制一份,然后Push到堆栈中。所谓Push,就像塞子弹一样把一个矩阵压入到堆栈中,此时,栈顶就是这个新的矩阵了,注意定义的向量都是和栈顶变换矩阵作用的。
-
glPopMatrix:将堆栈的栈顶变换矩阵Pop出来。
该讲的讲完了,下面出几道题目练习下吧。
1、OpenGL代码是:glLoadIdentity(); glTranslate3f(4,5,1); glRotate3f(0,1,0,90); glVertex3f(1,1,1); 请问此时栈顶变换矩阵是什么?(1,1,1)这个点到了OpenGL世界中的点是什么?
答:栈顶变换矩阵是T(4,5,1)*R(0,1,0,90),(1,1,1)到OpenGL世界中的坐标是T(4,5,1)*R(0,1,0,90)*(1,1,1).
2、解释为什么使用glPushMatrix和glPopMatrix的组合可以隔离这两个函数中的变换,使之不影响后面的点?
答:glPushMatrix新压入的变换矩阵是复制了原来的栈顶变换矩阵,所以它继承了之前的变换,此后执行glTranslatef、glRotatef这些函数时,修改的是栈顶变换矩阵,在glPopMatrix之前的点都将受到栈顶变换矩阵的作用,之后用glPopMatrix,把栈顶变换矩阵Pop掉,此时的栈顶变换矩阵又还原成原来的那个栈顶变换矩阵。
3、为什么有时候glTranslate3f和glRotate3f能颠倒有时候又不能?
答:矩阵A乘以矩阵B未必等于矩阵B乘以矩阵A,当它们有相等的时候,很多时候这只是巧合。