集合的性质在证明扩展欧几里德和欧拉定理的表现

这些是最基础的数论知识，写出来是强调集合性质的表现。集合中的元素是无序的、互异的。函数是一个集合到另一个集合的映射，对于原象中的任何一个元素，至多有一个元素与之对应。

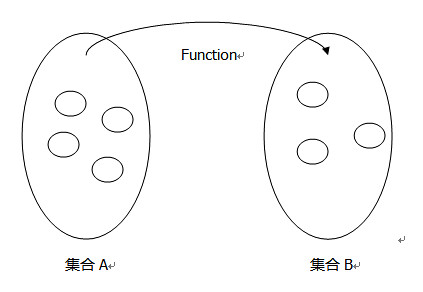
集合A是原象，集合B是象。抽屉原理就是运用集合的性质，如果集合A的元素比集合B多，则集合A至少存在有两个以上的元素，映射到相同的一个元素（集合B中）；如果集合A的元素比集合B少，则集合B中比存在元素，不是从集合A映射过去的（不落在函数的值域内）。

扩展欧几里德算法：如果整数f >= 1，gcd(d,f)=1，那么d有一个模 f 的乘法逆元d’，即对小于f的正整数d，存在一个小于f的整数d’，使得d*d’ ≡1 mod f. 其中gcd(d,f)表示d和f的最大公约数。

例如：对于f=9，d=5，满足gcd(5,9)=1，则存在一个数d’< f，使得5*d’≡1 mod 9. 可以穷举出d’=2.

证明：

对于命题中的d*d’ ≡x mod f，可以把左边看成集合A，右边看成集合B，它们之间有一种一一对应的关系。

左边集合：d’的取值有0、1、2….f-1共f种可能。右边集合：x可能取0、1、2…f-1共f种可能。

反证法，假设对于所有的d’，不存在d’，使得d*d' ≡1 mod f. 那么集合A的元素数量就比集合B多。根据抽屉原理，必存在不同的d’，记为d1’,d2’，使得d*d1'≡d*d2'≡a mod f，a是落在0、2~f-1的某个值。d*d1'≡d*d2'≡a mod f等价于d*(d1'-d2')≡0 mod f，由于gcd(d,f)=1，则有(d1’-d2’)≡0 mod f，由于d1’和d2’落在0~f-1的范围内，所以(d1’-d2’)的取值范围为-(f-1)~(f-1)，则(d1’-d2’)只能为0，则有d1’=d2’。矛盾，所以存在d’，使得d*d’ ≡1 mod f，得证。

欧拉定理：网上广泛流传着这个证明。看的时候记得考虑一下集合的性质。