这是大三我在做数学物理方程作业时发现的，该结论可使那道证明题变得很简便，可惜考试时我没把该结论证明一遍，太懒了被扣分。
只要两个平行平面都切到球，则可以找到该球的一条直径，使得它和两平行平面垂直。因此命题也可表达成：对于球的任意一条直径，在其上面任取两点，过这两点分别作两个和该直径垂直的平面，则两平面切得的球表面积（不包括切平面面积）和这两点间的距离成线性正比。
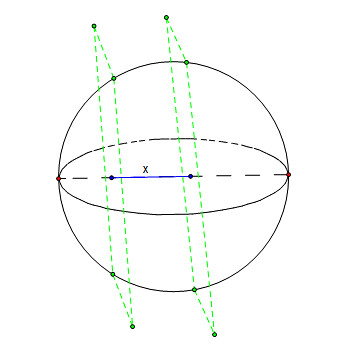
这个比例是2πr，r是球的半径。即图中距离x的两点的垂直平面切得的球表面积是2πr*x，只要两点落在直径上，无论两点距离多远，无论两点在什么位置上。
证明：
先求球冠的表面积，如图：
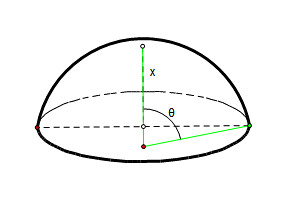
图中的红点是球心，x是球冠的高，θ是夹角。如图，对于角θ，其微分Δθ对应的弧长是r*Δθ，此时该切面的周长为2π*r*sinθ，则这一小圈表面积为r*Δθ*2π*r*sinθ，则球冠的表面积就是角θ从θ角度到0角度的积分。即：
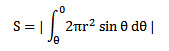
现在需要把θ换成x。首先
。当θ从θ积分到0时，x从x积分到0，dθ和dx的关系推导如下：
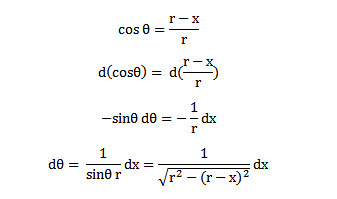
将上面的两条等式替换到S的表达式后，记得dx是从x到0，则有最后结论
。
利用该结论可以证明最终命题。记直径上的两点为x1和x2，到圆冠顶部的距离分别为x1和x2，则球面面积减去这两个圆冠的面积 = 两平面切得的球表面积。
两平面切得的球表面积 = 4πr^2 - 2πr*x1-2πr*x2 = 2πr*(2r-x1-x2)，而(2r-x1-x2)就是两点间距离。证毕。